How to Solve Cubic Equations Using Factor Theorem and Graphs?

26 May 2022 4816 share it:

If there’s one subject that takes a toll on most of the students, then it’s mathematics. It has been regarded as a subject that requires much skills, labor, and proper planning. Being a leading assignment writing service provider, we have been approached by many students everyday who ask us to help them solve their math equations and problems. We are always glad to assist them because we want them to secure sky-high marks.

Through this blog, we are trying to help those students who face issues in solving cubic equations. If such equations get on your nerves too, then you must take a read through the following the methods to understand how to solve a cubic equation. But before that, let’s discuss what a cubic equation is.

What Is a Cubic Equation?

A cubic equation is an equation which can be represented in the given form:

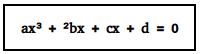
Here, a, b, c, d can be any number (may be complex if given so), but the value of a can’t be zero (a ≠ 0). All cubic equations either have three real roots (solutions) or just one that may or may not be equal.

One of the easiest ways to solve a cubic equation is reducing it to a quadratic equation, and then solving it either by factorizing or using the formula. But here, we’ll give you cubic equation solutions with steps using factor theorem and graphs. So, let’s get started.

How to Solve Cubic Equations Using Factor Theorem?

Factor theorem is a theorem that links factors and zeros of a polynomial. It is the result of the polynomial remainder theorem, and is based on the same reasoning. It states that a polynomial f (x) has a factor (x - a) if and only if f (a) = 0 (i.e. a is a root).

Now, through the following example, we’ll explain you how to solve a cubic equation algebraically.

Example:

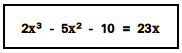
First of all, we need to equate the equation to zero. For that, we will subtract 23x from both the sides. So, our equation will be-

2x³ - 5x² - 23x - 10 = 0

Now, let’s assume that f (x) ≡ 2x³ - 5x² - 23x - 10

We’ll now factorize 2x³ - 5x² - 23x - 10 using the factor theorem.

We’ve to find the values of ‘x’ which would prove that 2x³ - 5x² - 23x - 10 = 0.

TRICK: Assume that the value of ‘x’ is the factor of 10 or -10.

So, if x = 1, then f (1) = -36

If x = -1, then f (-1) = 6

x = 2, then f (2) = -60

And, if x = -2, then f (-2) = 0

Therefore, (x + 2) is a factor of f (x).

Now, we can express 2x³ - 5x² - 23x - 10 = 0 as-

(x + 2) (ax² + bx + c) = 0, where a = 2, b = -9, c = -5

So, (x + 2) (2x² - 9x - 5) = 0

If we factorize this equation further, then we’ll have-

(x + 2) (2x + 1) (x - 5) = 0

This means, anyone of these expressions can be equal to zero.

Therefore, x = -2, x = -1/2, x = 5

How to Solve Cubic Equations Using Graphs?

Other than the factor theorem, you can try solving cubic equations using graphs. Start by drawing an accurate graph of the cubic equation. The points where the line of the graph intersects the x-axis will be the roots of your cubic expression. However, the accuracy of the solution will depend upon the accuracy of your graph.

We’ll now show you through the following example how to solve 3 degree cubic equation and find its roots easily using graphs.

Example:

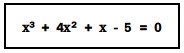
We will first draw a graph of y = x³ + 4x² + x - 5

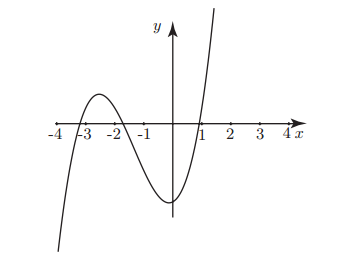
The graph intersects the x-axis at three places, so there are three real roots of this cubic equation. Hence,

So, this is how you can solve any cubic equation using the factor theorem and graphs. While solving cubic equations, you need to be very focused and organized as little confusions can lead to wrong solutions.

We have a team of experts who can provide you with assignment help for any subject.

If you are still confused how to solve cubic equations by hand, then we suggest you to take help from our mathematics assignment writing experts. Since they hold the highest academic credentials in mathematics, finding solutions of cubic equations is like a cakewalk for them. So, approach us today to make your dream of scoring high in mathematics assignments come true!